Kutha Ardana Blog: Happy Fibonacci Day, 11/23

November 23, atau 11/23 sering dikenal sebagai hari Fibonacci, karena keempat digitnya membentuk barisan/bilangan Fibonacci {1, 1, 2, 3, 5, 8, ...}. Bagaimana asal muasal munculnya barisan Fibonacci serta aplikasinya dalam dunia nyata?

Pada tahun 1202, Leonardo Fibonacci (Italia) dalam bukunya Liber abaci menulis sebuah teka-teki menarik sebagai berikut: Berapa banyaknya pasangan kelinci dalam setahun yang dihasilkan oleh sepasang kelinci jika setiap bulannya menghasilkan sepasang kelinci baru? Jawabannya menghasilkan barisan Fibonacci seperti diperlihatkan pada ilustrasi gambar berikut.

Masing-masing bilangan dapat diperoleh dengan menjumlahkan dua bilangan sebelumnya, sehingga barisan Fibonacci dapat dibangkitkan dengan mendefinisikannya secara rekursif

$$F_1=F_2=1,F_n=F_{n-1}+F_{n-2}, n \geq 3$$

Perintah Fibonacci[n] dalam Mathematica akan menampilkan bilangan Fibonacci ke-n.

Table[Fibonacci[n],{n,15}]

{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610}

Fibonacci dan Golden Ratio

Salah satu konstanta penting dalam matematika adalah golden ratio, `phi`, yang banyak digunakan dalam rancang bangun bentuk-bentuk geometris yang mempertemukan konsep matematik dengan nilai estetika yang tinggi (lihat: Golden Ratio di Balik Keindahan).

GoldenRatio//N

1.61803

Untuk nilai n yang besar, nisbah $F_{n+1}/F_n$ akan menghasilkan golden ratio.

Table[Fibonacci[n + 1]/Fibonacci[n], {n, 20}] // N
ListPlot[%, PlotRange -> All, Joined -> True, PlotLabel -> F[n+1]/F[n]]

{1., 2., 1.5, 1.66667, 1.6, 1.625, 1.61538, 1.61905, 1.61765, 1.61818, 
1.61798, 1.61806, 1.61803, 1.61804, 1.61803, 1.61803, 1.61803, 1.61803, 
1.61803, 1.61803}

$F_{2n-1},n \geq 2$, yakni $\left \{ 5,13,34,...\right \}$ adalah panjang sisi miring segitiga siku-siku. Contoh: $5^2=3^2+4^2, 13^2=5^2+12^2, 34^2=16^2+30^2,...$

Sebarang empat bilangan Fibonacci berurutan $F_n,F_{n+1},F_{n+2},F_{n+3}$ dapat digunakan untuk membentuk tripel Phytagoras dengan formula

$$a=F_n F_{n+3},b=2F_{n+1}F_{n+2},c=F_{n+1}^2+F_{n+2}^2,a^2+b^2=c^2$$

Aplikasi

Bilangan Fibonacci muncul, baik di alam maupun di banyak analisis atau metode terutama dalam bidang komputasi. Di alam, barisan Fibonacci banyak ditemukan pada pola percabangan pohon, susunan daun pada sebuah dahan, banyaknya petal pada beberapa kembang, banyaknya spiral pada nenas, dll. (lihat: http://en.wikipedia.org/wiki/Fibonacci_number)

Dalam bidang keilmuan lainnya:

computational run-time analysis pada algoritme Euclid untuk menentukan pembagi persekutuan terbesar dari dua bilangan bulat,
pembangkitan bilangan acak (pseudorandom),
polyphase merge sort,
teknik pencarian Fibonacci - sebuah metode pengoptimuman berdimensi satu,
sebagai barisan lengkap: semua bilangan bulat positif dapat dinyatakan sebagai penjumlahan satu atau beberapa bilangan Fibonacci secara khas sehingga penjumlahannya tidak melibatkan dua bilangan Fibonacci yang berurutan (Teorema Zeckendorf),
sistem perdagangan: Fibonacci Retracements, Arcs, and Fans,
penentuan tuning dalam musik.

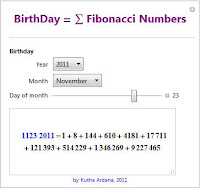
Demo: Tanggal Lahir Sebagai Jumlah Bilangan Fibonacci

Berikut adalah implementasi dari Teorema Zeckendorf yang diaplikasikan untuk tanggal lahir. Teorema ini menjamin tanggal lahir anda dapat dinyatakan secara unik sebagai penjumlahan beberapa bilangan Fibonacci yang berbeda . Algoritme yang digunakan berasal dari David Ter. Implementasi untuk bilangan bulat berurutan dapat dilihat di "Zeckendorf Representation of Integers" from the Wolfram Demonstrations Project.